3. Mathematics
3. Mathematics
3.1 Mathematics
- Understand addition, subtraction, multiplication and division.
- Understand fractions, proper, improper and decimal. Understand powers of 10 (scientific notation).
- Recall units and sub-units; (tera, giga, kilo, UNIT, milli, micro, nano, pico) and conversion to and from each.
- Understand squaring and square roots. Understand reciprocals.
- Understand graphs and be able to interpret them.
Addition and Subtraction
In any maths problem it must be remembered that a number without a plus or minus sign written against it is assumed to be a positive number.
5 + 5 = 10 is really (+5) + (+5) = (+10)
Every number has a decimal point. A whole number such as 6 is six point zero (6∙0), and for convenience sake we normally don’t show the decimal zero. However it is just as correct to write 6∙0000000000 as 6, the number is the same.
When adding numbers of the same sign the result will have the same sign as the numerals.
5+2 = 7 or (+5) + (+2) = (+7)
(-5) + (-2) = -7
When subtracting numbers of the same sign the result will not always be as obvious. We are all familiar with five minus three equals two or (+5) – (+3) = (+2).
(-5) – (-2) = (-3) may not be a major problem but
(-2) – (-5) = (+3) could be confusing.
It may be easier to treat all subtraction problems as additions after working the signs.
Like signs may be treated as a plus. That is to say – (-5) is the same as +5.
Using the above example :
(-2) – (-5) the – (-5) being like signs become a + and we have
(-2) + 5 and the answer becomes a little more obvious as +3
Similarly (-5) – (-3) becomes (-5) + 3 = -2
When adding values with different signs remember:
- The problem will always be done as a subtraction of the smaller number from the larger number.
- That the resultant sign will be the same as that of the highest value in the problem.
- When a number is shown without a sign it is assumed to be positive.
Examples:
- (-5) + (+3) = -2
Subtract the smaller number from the larger [5-3 = 2]
Apply the sign of the larger number [-2]
- (-3) + (+5) = 2
Subtract the smaller number from larger [5-3 = 2]
Apply the sign of the larger number [+2 or 2]
Fractions
The terms numerator and denominator are used to indicate a part of a fraction. The numerator is the part of the fraction above the fraction bar.
The denominator is the part of the fraction below the fraction bar.
1 Numerator
/ Fraction Bar
2 Denominator
Proper Fractions
Proper Fractions are those which indicate a part of a whole.
1/3 indicates that the whole number is divided into 3 parts and only
one part is present.
It means the same as 1 divided by 3 and could be written as 1÷3
Often fractions can be simplified by dividing the numerator and denominator by the same number.
For example:
3/6 is the same as 1/2 both denominator and numerator have been divided by 3.
8/32 = 4/16 = 2/8 = 1/4 both have been divided by two and two and two again.
Improper fractions are those that indicate a complete number and parts.
4/3 indicates that there is one whole (3/3) and 1/3. This can be simplified to 11/3
40/32 = 20/16 = 10/8 = 5/4 = 11/4 or
40/32 = 1 8/32 = 14/16 = 12/8 = 11/4
A decimal is merely another way of expressing a fraction to the base ten.
0∙1 is 1 divided by ten, 1/10 or one tenth.
0∙5 is 5 divided by ten, 5/10 or simplified to 1/2 or one half.
The number of decimal places indicates the number of zeros in the denominator.
0∙1 is 1/10 : 0∙01 is 1/100 : 0∙001 is 1/1000 : 0∙00001 is 1/100000
As with whole numbers, 0∙5 could be written as 0∙50 or 0∙500,
Examples:
0∙50 is 50/100 which is the same as 5/10 or 0∙5
0∙500 is 500/1000 which is the same as 50/100 (or 0∙50) or 5/10 (or 0∙5).
Powers of Ten
As we saw when squaring a number ten squared is one hundred (102 = 100).
This can be expanded by using higher exponents such as 103 equals 1000
(10*10*10. 10*10 = 100; 100*10 = 1000).
106 = 1000000 ( [1] 10*10 = 100; [2] 100*10 = 1000; [3] 1000*10 = 10000;
[4] 10000*10 = 100000; [5]100000*10 = 1000000.
Note: The exponent does not indicate the number of times the number is multiplied but the number of times the number is used.
In 103 there are only two ‘*’ steps but the 10 is used three times and in the 106 there are five ‘*’ steps. the first step uses 10 twice (10*10) and each ‘*’ step after that uses 10 once so only five ‘*’ steps are used to multiply 10 by itself six times.
These exponents with a base 10 may be used with another number, such as 6x103. This is 6*10*10*10 or 6000.
(6*10 = 60; 60*10 = 600; 600*10 = 6000. Again the exponent shows how many times 10 is used in the multiplication process.
Exponents may also be used in the negative, such as 10-3. The minus sign in front of the exponent indicates that the number is divided by 10 to the power shown. In this case,
divided by 103 or 1000, so 10-3 is 1/1000. If combined with another number (5*10-3) it indicates the number (5) divided 1000 or 5/1000.
Another way of writing exponents with a base 10 is to use the letter E in place of the 10.
5*103 could be written as 5E3 meaning five multiplied by ten to the power of three.
Note the E means a power of ten so 2E2 is NOT 22 (4) but is 2*102 (200).
Convert 6 000 000 000 (There are nine zeros = E9) = 6E9
Convert 3E6 (E6 indicates six zeros) = 3 000 000
NOTE: In electronics we usually work with exponents in the multiple of 3 (E3, E6,E9 etc) because they equate to the SI Prefixes (to be explained shortly). but remember that exponents may be 2E2 (200) which is the same as 0∙2E3 (200) or 20E1 (200).
S.I. Units
When using the decimal system any unit (meter, litre, gram etc) can be prefixed with an indicator to show larger or smaller amounts. Many of these are in common usage such as kilometre (1000m), millilitre (1/1000 ). The prefixes remain the same, regardless of the unit or what is being measured. Kilo can be applied to any measurement meaning a thousand of that unit whether it is a gram, meter, litre or snazzle. The only place where these are not used is in time measurement of greater than a second and less than a year.
They can however be used to indicate time of less than a second.
The prefixes go as high as Exa (1E18) and as small as atto (1E-18). In this course we are only concerned with units between Tera (1E12 and pico (1E-12).
Prefix Number Power of ten
Tera (T) 1 000 000 000 000 1E12 (1x*10^12 or 1*1012)
Giga (G) 1 000 000 000 1E9 (1*10^9 or 1*109)
Mega (M) 1 000 000 1E6 (1*10^6 or 1*106)
Kilo (k) 1 000 1E3 (1*10^3 or 1*103)
Unit 1
Milli (m) 1/1000 or 0∙001 1E-3 (1*10^-3 or 1*10-3)
Micro (μ or u) 1/1 000 000 or 0∙000 001 1E-6 (1*10^-6 or 1*10-6)
Nano (n) 1/1 000 000 000 or 0.000 000 001 1E-9 (1*10^-9 or 1*10-9)
Pico (p) 1/1 000 000 000 000 or 0.000 000 000 001 1E-12 (1*10^-12 or 1*10-12)
When using these prefixes it is usually easier to work in decimals than fractions.
To convert one unit to another it is a matter of moving the decimal place to the left or right. To convert 5000m to km the decimal place moves three places to the left leaving us with 5km. Starting with 5 0 0 0 ∙ 0m
5 0 0∙0 is one place
5 0∙0 is two places
5∙0 is three places
If converting in the other direction, 5km to m the decimal is moved in the opposite direction so 5∙0km becomes 5000∙0m. The decimal point and the following zero are normally not written in so 5km = 5000m.
Once the units scale is known the rule becomes:
If moving upward on the scale the unit (1) the decimal point moves to the left three places for each prefix.
So if converting 7pF to nF. The scale goes pico, nano, micro, milli, 1, kilo etc so we are moving upward on the scale by one prefix so the decimal point moves to the left three places.
7∙0; move one place = 0∙7 ; the second place = 0∙07 ; third place = 0∙007nF
Convert 600kV to MV. Moving upward on the scale by one prefix the decimal point moves to the left by three places. 600; moving one place = 60∙0; second place = 6∙00; third place = 0∙600. 600kV = 0∙6MV
Convert 3nF to mF. In this case we are moving through 2 prefixs (n, μ, m) so the decimal moves six places to the left. 3nF = 0∙000 003 mF.
If moving downward on the scale the decimal moves to the right three places for each prefix.
Convert 4MV to V. Moving down the scale move by two prefixes move the decimal point six places to the right. One place = 40; two places = 400; three places = 4 000; four places = 40 000; five places = 400 000; six places = 4 000 000. 4MV = 4 000 000V
Convert 500μH to pH. Moving down on the scale by two prefixs – move the decimal 6 places to the right. One place = 5 000; two places = 50 000; three = 500 000; four = 5 000 000; five = 50 000 000 and six = 500 000 000. 500μH = 500 000 000pH
Convert 6km to m. Moving down on the scale the decimal point moves to the right. One prefix so it moves three places. 6km = 6 000m
Square of a Number
A square of a number is the number multiplied by itself and is indicated by a superscript figure 2 following the number (called the exponent). For example 3 squared would be written 32. Because putting in a superscript is not always possible it may be written as 3^2 (the ^ indicates following number(s) are in superscript).
This indicates that the 3 is multiplied by itself that is 3*3 = 9.
102 = 100 or 10*10
Note: The number is not multiplied by the exponent but by itself.
The square root of a number is the opposite of the square of a number. That is to say the square root (written as √ ) of a number is the number which is multiplied by itself to give the original number.
For example √4 is 2 (because 2*2=4) or the √9 = 3 (3*3=9).
For small simple numbers these can be calculated from ‘times tables’ learnt in primary schools but for larger or more complicated numbers a calculator is required.
Operations with exponents
When multiplying two numbers with exponents, the numbers are multiplied and the exponents are added.
2E3*2E3 The numbers (2*2) are multiplied as normal (4)
The exponents (E3 and E3) are added (E6)
giving a result of 4E6.
This can be proved by converting the original problem to whole numbers and multiplying:
2E3*2E3 = 2000*2000 = 4 000 000 or 4E6
Examples:
Resolve 5E3*2E6
Multiply the numbers (5*2) = 10 and add the exponents (E3+E6) = E9 gives 10E9
Resolve 3E6*2E-3
Mulitply the numbers (3*2) = 6 and add the exponents (E6+E-3) = E3 gives 6E3
Resolve 4E-6*2E3
Multiply the numbers (4*2) = 8 and add the exponents E-6+E3 = E-3 gives 8E-3
When dividing numbers with exponents, the numbers are divided and the exponents subtracted.
4E9 ÷ 2E6 or 4E9/2E6 The numbers are divided (4÷2) = 2
The exponents are subtracted (9-6) =3
Result 2E3
Prove: 4 000 000 000 ÷ 2 000 000 = 2000 or 2E3
Resolve 4E-6÷2E-3 The numbers are divided (4÷2)=2 and exponents are subtracted
(-6-(-3)) = -3. Giving 2E-3
Resolve 6E-6÷2E-3. 6÷2 = 3 and E-6 – E-3 = E-3 giving 3E-3
Reciprocals
The reciprocal of a number is that number inverted. That is to say if we take any number as a fraction and turn it upside down.
For example 2 as a fraction is 2/1 , turned upside down it becomes 1/2 .
The reciprocal of two is one half or 0∙5.
Similarly the reciprocal of 0∙5 is 2. 0∙5 as a fraction is one half (1/2) when inverted
becomes 2/1 or 2
To put it another way the reciprocal of a number is one divided by that number.
The reciprocal of 2 is 1÷2 or 1/2 or 0∙5.
The reciprocal of 0∙5 is 1÷0∙5 or 1/0∙5 or 2
The reciprocal of 5 is 1/5 or 0∙2
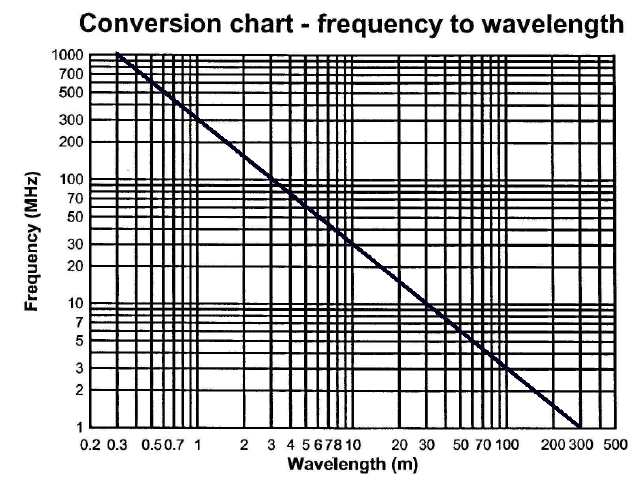
Graphs - (see examples on the left)
Graphs are merely pictorial representations of one function versus another.
[see conversion chart - frequency to wavelength on the left]
The frequency represented on the vertical axis and the wavelength on the horizontal with the diagonal line showing the relationship intersection.
To use this type of graph find the frequency required and trace horizontally to the relationship intersection line then vertically to the wavelength scale and read the result. To convert wavelength to frequency, find the wavelength on the bottom scale and trace up to the intersection line then horizontally to determine the frequency.
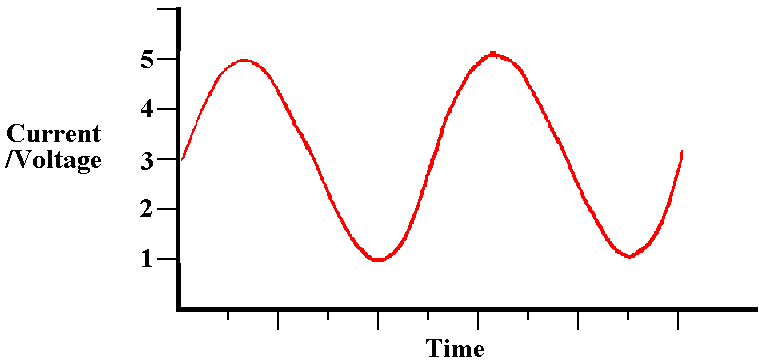
A graph where voltage/current is shown in relation to time. [see to the left]
To translate this type of graph firstly the time interval markings must be known. If we assume they are 0∙5 seconds and we wish to know the voltage at 2 seconds.
Find the second point on the horizontal scale (fourth mark) and trace vertically until intersection with the sine wave and trace horizontally to read the vertical scale. The result is 1V.
To find the time at which the voltage is 4V trace a line horizontally from the 4 on the vertical scale to intersection with the sine wave and drop vertically to read the time on the horizontal scale.
NOTE: There are several times when this occurs and unless further specification is given the answer will be 0∙2, 1∙1, 2∙7 and 3∙6.
It is possible to predict occurrences using a graph such as this.
For example: Calculating the time between existing 4v points. While the wave goes through its peak voltage there is 0∙9 seconds between existing 4V points and while the wave goes through the minimum voltage there is 1∙6 seconds between 4V points, so by adding the time through minimum voltage the next 4V peak should appear at 3∙6 + 1.6 seconds and the one after will be at 3∙6 + 1∙6 + 0∙9. They should occur at 5∙2 secs and 6∙1 secs.
Formulae Transposition (optional)
When dealing with a large number of formulae it is virtually impossible to remember all the variations of each formulae. It is essential to be able to transpose, or move the formulae around so as to obtain the desired result.
If we take the Ohms law formulae (V=IR), we may be able to remember the three variations of it, V=IR; I=V/R and R=V/I but when we come to trying to remember all the variations of several long formulae, which are similar, it becomes much harder. It is necessary to be able to manipulate, or transpose formulae.
If we look at a maths problem: 8 = 16/2 it makes perfect sense.
We can transpose that to read 8*2 = 16.
When using simple figures this will appear obvious, but what have we really done mathematically?
We have multiplied both sides of the equation by two. On the left hand side 8*2, and on the right 16/2 * 2/1 = 32/2 = 16 ( another way of explaining it is that the 2 numerator cancels the 2 denominator leaving 16/1 which is 16).
As long as we do the same thing to both sides of the equation it will remain true.
Manipulating letters in the same way is the basis of transposing equations.
It is important to remember that a letter in an equation is really a number, the reason we use a letter is because it hasn’t been given a specific value yet but it represents a relationship with another value also represented by a letter.
In Ohms law for example the relationship between the three letters is true regardless of the figures actually present or used.
Using Ohms law formulae, V = IR, (or V = I*R the multiplied sign is assumed to be there if nothing is written) we can transpose this into two other formulae.
If we wish to make I the subject of the formulae, that is to say, we are given V and R and have to find I.
V = IR and we wish to leave I on its own (make it the subject), we must remove the R from the right of the equation. If we divide both sides by R we get:
V/R = IR/R R/R will equal one (any number divided by itself must equal 1) Leaving:
V/R = I
V = IR and we wish to find R. Divide both sides by I (V/I = IR/I) leaving us with V/I = R
It does not matter whether we say V/I =R or R=V/I the result is the same.
Another example:
P=VI Find I
Divide both sides by V to leave I on its own
P/V = VI/V or P/V = I
Using a more complex formulae the process is the same:
If X = PfHt Find H. As before we must isolate H so both sides must be divided by P, f and t. This can be done in individual steps: –
- Divide both sides by P ( X/P = PfHt/P )
- Remove the p divided by p (X/P = fHt )
- Divide both sides by f ( X/Pf = fHt/f )
- Remove the f/f (X/Pf = Ht)
- Divide both sides by t (X/Pft = Ht/t)
- Remove the t/t (X/Pft = H)
The procedure is the same with any formulae.
Another complex formulae:
Z = √(R2 + X2) The brackets around the R2+X2 indicate that the √ applies to all the objects within the brackets, this means that to resolve this the R and X must be squared and added before the square root can be applied.
To substitute figures: If R=4 and X=4 then the equation should be solved as:
Z = √ (42 +42) = √ (16+16) = √32 = 5∙65
When transposing parts of this formulae the procedure is reversed or the square root must be removed from the right of the formulae before anything can be done with the parts within the square root sign.
A square root that is squared is the original number
Mathematically √42 =√ (4*4) = √16 = 4.
Also in this formulae ( Z=√(R2+X2) we are adding not multiplying.
To remove an addition the value must be subtracted whereas when multiplying it is divided.
To put that mathematically:
To transpose 3*3 = 9 we divide by 3 on both sides giving 3 = 9/3
to transpose 3+3 = 6 we subtract 3 on both sides giving 3 = 6-3
Z = √(R2 + X2) Find R
Firstly remove the square root by squaring both sides Z2 = (√(R2+X2))2
On the left the square root is cancelled by the square Z2 = R2+X2
Subtract X2 from both sides Z2 – X2 = R2+X2 − X2
X2 − X2 cancel each other Z2 − X2 = R2
Square root both sides to remove the square from the R √(Z2−X2) = √R2
The √ and 2 on the right cancel each other √(Z2 − X2) = R
When doing any transposition of formulae it is a good check to substitute simple numbers at the start and end of the transposition to check that it has been done correctly.
As examples using the formulae we have transposed above:
- V=IR to I = V/R
If we substitute simple figures in the first equation then using the same figures the second should hold true. If we say I and R both are 2 then V will be 4
Then in the first equation (V = IR ) 4 = 2*2
In the transposition ( I = V/R ) 2 = 4/2 giving 2=2
Mathematically true so the transposition has been done correctly
- X = PfHt
Again if we use 2 for the value of all the items on the right of the equation
X = 2*2*2*2 or 16 = 2*2*2*2
Using the transposed formulae of X/Pft = H If we substitute the figures we have 16/2*2*2 = 2
2*2*2 = 8 so we have 16/8 = 2 giving 2=2
Mathematically true so the transposition has been done correctly.
- Z = √(R2 + X2)
Z = √( 22 + 22 ) = √ (4 + 4) = √8 = 2∙828
Transposed √(Z2 − X2) = R
√(2∙8282 − 22) = 2
√(8 − 4) = 2
√4 = 2
2 = 2
Mathematically correct so the transposition has been done correctly.
Ratios (optional)
A ratio represents a relationship between two quantities and is usually written as 2:1. This indicates that whatever value the left hand side has, the value on the right will always be half of that left value. The same ratio can be indicated by any pair of figures as long as the right is double the left, such as 4:2; 8:4; 20:10; 400:200. The primary ratio in all these is 2:1.
The important thing with ratios is to realize that the ratio can be considered as the total number of parts into which a whole divides. That is to say that if three is to be divided into a ratio of 2:1 the whole (three) is divided into three parts 2:1. Similarly five divided into a ratio of 2:1 is divided by three and distributed as 2/3 : 1/3 or 3∙3:1∙6
18 divided into a ratio of 7:2
7:2 is a total of 9 parts (7+2=9)
18 divided by nine gives 2 per part
The parts are proportioned as 7 parts (7*2 = 14)
and 2 parts (2*2 = 4)
18 divided into a ratio of 7:2 is 14:4
Divide 64 into a ratio of 5:3, resolves to 5/8 *64 : 3/8*64 or 40:24.
Another problem involving ratios comes about when part of the ratio is given and the other part has to be found or the total value.
In a ratio of 3:2 the left side has a value of 15. What is the value of the other side and the total?
In a ratio of 3:2 the total value is divided into five and proportioned as 3 parts to 2 parts or
So we are told that the left side ( 3/5 of the total) has a value of 15. So 1/5 will be 15÷3 or 5
The right side is 2/5 or 2*5 = 10
The proof of this is that 15:10 reduces to 3:2 (both sides divided by 3).
The total is obviously the right side plus the left or 10+15=25
In a ratio of 7:2 the right hand side has a value of 6. What is the value of the left hand side and the total value?
6=2/9 of the total therefore 1/9 = 3 (6÷2) and 7/9 =21 (3*7)
The values are 21:6 (To prove - dividing both sides by 3 gives the original ratio - 7:2)
The total value is the sum of both sides 21+6=27
So far we have only worked ratios between two values but they may be expressed with any number of values. A ratio of 5:3:2:4:12 can be worked with in exactly the same way as the two value ratios above.
If fifty two is to be divided into the above ratio, firstly calculate the number of parts in the ratio. 5+3+2+4+12 = 26. Fifty two divided by twenty six is two so each part is worth 2 so the 54 divides as 10:6:4:8:24.
If given one of the ratio values say the second value (3) is six. 3/26 = 6 then 1/26 = 2 so the ratio resolves as 10:6:4:8:24 and the total is 10+6+4+8+24 = 52
Directly Proportional and Inversely Proportional (optional)
These are two terms which need to be understood in relation to formula.
If we say that two items in a formula are directly proportional it indicates that if one item is increased (or decreased) the other will increase (or decrease) in a direct relationship.
Example: I = V/R I is directly proportional to V
If we raise V by doubling it then I will double
It will not necessarily be the same amount of change but by the same proportion.
In figures: 8 = 16/2 Raising V by 8 will not cause I to increase by 8 but by a direct proportion.
8 is one half of 16 so I will increase by half its value or 4.
12 = 24/2 16 has been increased by half its value (8) and so 8 increases by half its value (4).
An inverse proportion is exactly the reverse. If one value decreases the other will increase by the same proportion.
Example: I = V/R I is inversely proportional to R
If we increase R then I will reduce. Again by the same proportion.
Figures; 8 = 16/2 If we increase 2 by doubling it to 4 the 8 will reduce by the same proportion. The inverse of 2 is ½ so 8 will reduce by ½ to 4.
4 = 16/4
